The user defined waveform allows an arbitrary waveform to be specified by importing a file or defining an equation.
Controls
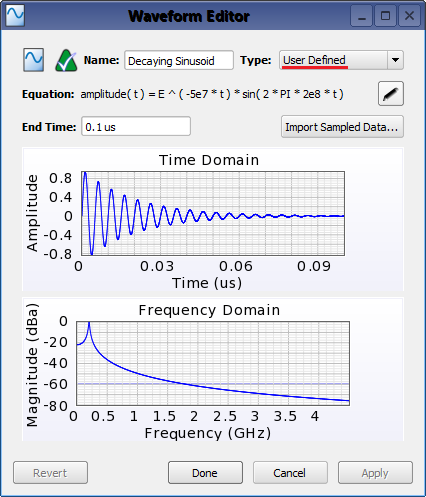
Double-clicking on a waveform in the Project Tree opens the Waveform Editor, where a user defined waveform is accessed by setting Type to User Defined. Once selected, controls for importing a file or defining an equation will appear.
If the waveform will be specified based on a file, click the Import Sampled Data button and select the file using the import window that opens. Once a file is imported, End Time will disable since this field only applies when an equation is entered.
Users should consider the following criteria when creating a file:
- The file should be a text file containing sampled waveform data.
- Any extension is allowed, i.e., *.src or *.txt.
- Each line of the file must contain a time in seconds, one or more whitespace characters, and the waveform amplitude at that time.
- The first line should start at time zero with an amplitude of zero, i.e., 0 0
- XF expects the last line to have an amplitude of zero, however, this is not a requirement. Step waveforms are supported by specifying the final value at a time later than the simulation will run.
Users can reference this double exponential waveform file for an example.
Alternatively, click the  button to open the Set Waveform Equation window. Here, the waveform can be entered as a continuous function of time. The built-in functions are documented in the equation editor in the lower half of the window. Once the equation is entered, the waveform's End Time must be specified. After this time, the waveform's amplitude is treated as zero.
button to open the Set Waveform Equation window. Here, the waveform can be entered as a continuous function of time. The built-in functions are documented in the equation editor in the lower half of the window. Once the equation is entered, the waveform's End Time must be specified. After this time, the waveform's amplitude is treated as zero.
For file-based and equation-based waveforms, the amplitude should not change rapidly. Transitions are required to prevent high frequency content from being injected into the simulation space and causing instability. For example, a true step waveform that jumps to 1 on the second line of an imported file or amplitude(t) = 1 should not be specified.
Example Equations
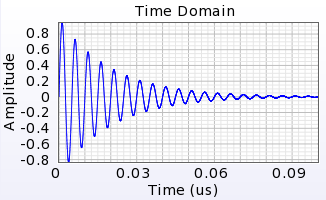
XF has multiple built-in functions, including sin(t), exp(t), and pow(x,y), as well as constants, such as PI, c, and E, that can be used when defining the waveform's equation. An exponentially decaying sinusoidal waveform utilizes both.
amplitude( t ) = E ^ ( -5e7 * t ) * sin( 2 * PI * 2e8 * t )
For readability, units can be entered into the equations as seen in the following double exponential waveform equation:
amplitude( t ) = exp( -t / 20 ns ) - exp( -t / 0.5 ns )
Further, parameters from XF's parameters list can be introduced. The tau1 and tau2 parameters were created with values of 0.5 ns and 20 ns, respectively.
amplitude( t ) = exp( -t / tau2 ) - exp( -t / tau1 )