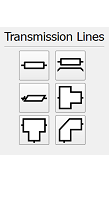
Set the properties of schematic elements.The workspace window of the schematic editor contains components and transmission lines for use when adding schematic elements to a project. Once added to the current schematic, users can edit a transmission line's properties by either double-clicking on the desired element in the schematic window, or right-clicking on the desired element and selecting Edit Properties.
Each transmission line property editor includes element-specific settings, as well as the following general options:
- Name: user-defined component identifier.
- Label Position: placement of a component's label.
: determines which information is visible in a component's label. - Enabled State: sets a component as either active or inactive. Inactive components are either open or short.
Ideal Transmission Lines
The 
button adds a two-terminal ideal transmission line to the current schematic.
The 
button adds a four-terminal ideal transmission line to the current schematic.
An ideal transmission line is defined by its admittance parameters as
\begin{equation} Y_{11} = Y_{22} = \frac {1} {jZ_0 \tan (\beta l_p)} \end{equation} \begin{equation} Y_{12} = Y_{21} = \frac {j} {Z_0 \sin (\beta l_p)} \end{equation}where $Z_0$ is the characteristic impedance, $\beta$ is the phase constant, and $l_p$ is the physical length of the line. The physical line length is calculated from the electrical length according to
\begin{equation} l_p = \frac {l_e} {360} \lambda = \frac {l_e} {360} \frac {c} {2 \pi f} \end{equation}where $l_e$ is the electrical length in degrees, $c$ is the speed of light in a vacuum, and $f$ is the transmission line's evaluation frequency in Hz.
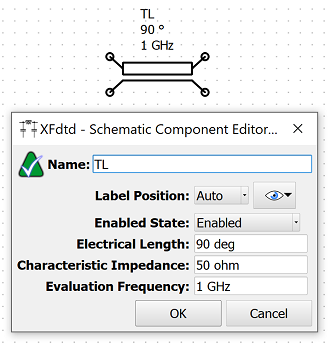
The following settings define the ideal transmission line parameters:
- Electrical Length: the electrical length, or phase length, defines the amount of phase shift an electromagnetic wave incurs while traveling over the length of the transmission line at a given frequency. The electrical length must be greater than zero.
- Characteristic Impedance: the characteristic impedance of the transmission line. The characteristic impedance must be greater than zero.
- Evaluation Frequency: the frequency at which the electrical length is defined. The evaluation frequency must be greater than zero.
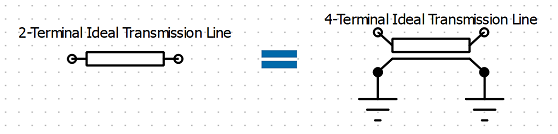
Users should note that the two terminal ideal transmission line assumes that the reference terminal of both the input and output ports is connected to global ground resulting in the relationship shown in the image.